Після вивчення матеріалу учень:
Обладнання: комп'ютери зі встановленими ОС та середовищем програмування мовою Python або стійким сполученням з Інтенетом для роботи з online-середовищами.
Структура уроку
3. Вивчення нового матеріалу
Бінарний пошук традиційно вивчають вже при першому знайомстві з масивами — див. опис.
Тернарний пошук використовують для пошуку:
максимума функції f на заданому проміжку [l, r] за умови, що функція спочатку строго зростає, потім досягає максимуму в одній точці або на відрізку, потім строго спадає;
мінімума функції f на заданому проміжку [l, r] за умови, що функція спочатку строго спадає, потім досягає мінімуму в одній точці або на відрізку, потім строго зростає.
Розгляномо лише перший варіант, бо інший абсолютно симетричний йому.
Алгоритм (тернарного пошуку максимуму за умови, що він досяжний лише в одній точці)
Вибрати довільні точки m1 і m2, що задовольняють нерівності: l < m1 < m2 < r. Наприклад, надати значень:
m1 = l + (r − l)/3;
m2 = r − (r − l)/3.
Порахувати значення функції f (m1) і f (m2).
Якщо f (m1) < f (m2) — шуканий максимум поза проміжком [l, m1) — надати значення:
l = m1.
Якщо f (m1) > f (m2) — шуканий максимум поза проміжком (m2, r] — надати значення:
r = m2.
Якщо f (m2) = f (m2) — шуканий максимум поза проміжками [l, m1) і (m2, r] при строгому зростанні й спаданні f до і після точки максимума при зростанні аргумента — надати значення:
l = m1;
r = m2.
Якщо r − l < ε, вивести значення (l + r)/2, значення f у цій точці і закінчити виконання алгоритму. Інакше перейти до пункту 1.
Тут ε — дійсне число — деяка наперед задана точність пошуку. Див. програму обчислення найбільшого значення функції f (x) = 1 − x2 на проміжку [−3, 2].
Пошук з поверненням. Деякі задачі можна розв'язати, лише перебираючи гіпотези. При цьому рівнів прийняття гіпотез може бути кілька. При переборі відкидають гіпотези у разі несумісності їх з умовою задачі. Інакше кажучи, задачу розв'язують оптимізованим перебором гіпотез. Це еквівалентно руху деревом можливих кроків алгоритму з відрізанням у разі несумісності з умовою відповідних гілок дерева. Рух здійснюють доти, поки не буде отримано шуканого розв'язку (чи всіх шуканих розв'язків) або встановлено, що розв'язків немає. Такий алгоритм називають алгоритмом з поверненням.
Програмне втілення алгоритму з поверненням проілюструємо на прикладі задачі з назаю «Хід коня». На шахівниці n × n клітин стоїть на полі (x, y) шаховий кінь. Потрібно знайти такий маршрут коня (ходити згідно із шаховими правилами) обходу всієї шахівниці із заходом у кожну клітин по одному разу.

Загальна структура алгоритму така: на кожному кроці аналізувати, чи можна ще зробити хід куди-небудь (перебирати всі варіанти). Якщо можливо, робити хід (приймати гіпотезу), якщо неможливо, повертатися на один хід назад (відхиляти останню прийняту гіпотезу). Так робити до тих пір, поки кількість відвіданих клітин не стане дорівнювати n 2.
Загальний вигляд основної процедури такого алгоритму такий:
//здійснення ходів з номером i з клітини (x,y)
def step (x,y,i):
# вибір ходу з клітини (x,y)
if (умова прийнятності ходу):
# здійснення ходу
if (умова існування результативного продовження, тобто
справдження step після зробленого ходу):
return Тrue;
else # відміна ходу
return False
У поданому вище тексті коментарі, виділені червоним кольором, потребують заміни на вказівки чи вирази, записані мовою програмування. Нижче описано, як це зробити.
Примітка. Функція step є рекурсивною: вона викликає сама себе.
Позиції можна описати за допомогою масиву h. Кожний елемент масиву h буде зберігати номер ходу, на якому було відвідано це поле, або -1, якщо «сюди кінь ще не ходив». Якщо змінні u, v описують позицію після можливого ходу з номером i, то маємо:
h[u*n+v]=i # запис ходу h[u*n+v]=0 # витирання ходу
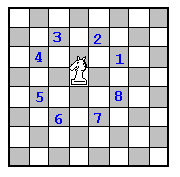
Опишемо (можливу) реалізацію схеми перебору ходів коня. Запровадимо сталі масиви dx, dy зі значеннями елементів −2, −1, 1, 2 у таких комбінаціях, щоб виконання вказівок:
u=x+dx[j]; v=y+dy[j];
при j = 1, 2, …, 8 відповідало ходу коня. Тут j — номер можливого майбутнього ходу.
dx = [2, 1,-1,-2,-2,-1, 1, 2] dy = [1, 2, 2, 1,-1,-2,-2,-1]
До першого звернення до процедури step потрібно заповнити масив h значенням -1 і надати значення:
h[x*n+y]=0;
Тут x, y — номери рядка й стовпчика клітинки, з якої кінь починає обхід таблиці (нумерація починається з нуля). У поданому прикладі коду x = y = 0. Лише після цього викликати процедуру:
step(x,y,1)
Перевірку умови прийнятності ходу можна записати таким чином:
if ((next_x >= 0) and (next_x < n) and (next_y >= 0) and (next_y < n)): if (h[next_x*n+next_y] == -1): …
— кінь не ходить за межі шахівниці та не ходить на поле, де він побував раніше (відмінені ходи не враховувати).
У поданому коді передбачено припинення виконання програми після знаходження й виведення першого розв'язку.
Результат виконання програми при n = 5 такий:
Є щонайменше такий розв'язок: 0 5 14 9 20 13 8 19 4 15 18 1 6 21 10 7 12 23 16 3 24 17 2 11 22
Характерним для реалізованого алгоритму є те, що під час пошуку розв'язку ми поступово:
Нерівності-порівняння для f (m1) і f (m2) змінити на протилежні за змістом.
Якщо однакові значення функції на кінцях поточного відрізка [l, r] такі самі, що й для попереднього відрізка, то мінімум функції досягається на цьому відрізку. Передбачити галуження для цього випадку.
Для знаходження меж найбільшого проміжку, на якому досягається мінімум функції, використати поділ (неперервного) діапазону значень між відповідними межами поточного й початкового відрізків.
Завдання 2. Створити програму пошуку з поверненням для дешифрації запису дії додавання ten + ten + forty = sixty.
Вказівка до виконання
Занумерувати літери у порядку першої появи при зростанні старшинства розряду.
Приймати гіпотези щодо значення змінної-літери у встановленому порядку.
Вести облік використаних цифр.
Можна використати вкладені цикли.
6. Підбиття підсумків уроку
Виставлення оцінок.
7. Домашнє завдання
Ознайомитися з умовами та ідеями розв'язання задач відбірково-тренувальних зборів команди міста Києва: 1.1, 4.2, 6.2, 15.2 (до крапки вказано номер завдання, після крапки вказано номер задачі) — див. посилання. Пересвідчитися у тому, що усі ці задачі розв'язано пошуком з поверненням. Звернути особливу увагу на задачу 6.2, в описі якої подано єдиний алгоритм оптимального розв'язання логічних задач. Звичайний пошук з поверненням (оптимізований перебір) без проміжних логічних висновків має істотно більший час виконання програми, ніж запропонований автором задачі.
Текст упорядкувала Чекман Тетяна Михайлівна, вчитель спеціалізованої школи № 64 Солом'янського району міста Києва, під час виконання випускної роботи на курсах підвищення кваліфікації з 10.12.2018 по 14.12.2018.