• ознайомити з принципами:
  • динамічного програмування;
  • жадібності алгоритму;
• описати процес розробки алгоритмів:
  • динамічного програмування;
  • жадібного алгоритму;
• ознайомити з програмним втіленням розглянутих алгоритмів;
• виробити навички програмного втіленням розглянутих алгоритмів.

Після вивчення матеріалу учень:

• пояснює: визначення й умови застосування принципів динамічного програмування;

• знає зміст понять: процес розробки, опис структури оптимального розв'язку, критерії застосування;

• розпізнає: задачі, що розв'язують з використанням динамічного програмування та жадібного алгоритму;

• уміє:
  • аналізувати та формулювати постановку задачі;
  • записувати коди розв'язання за алгоритмом;
  • розбивати завдання на підзадачі;
  • обчислювати оптимальні значення параметрів для всієї задачі;
  • створювати програми;
  • аналізувати результати виконання програм;
  • налагоджувати програму.

Обладнання: комп'ютери зі встановленими ОС та середовищем програмування мовою Pascal.

Структура уроку

1. Організаційний момент.
2. Актуалізація опорних знань.
3. Вивчення нового матеріалу.
4. Інструктаж з ТБ.
5. Вироблення практичних навичок.
6. Підбиття підсумків уроку.
7. Домашнє завдання.

• тип елементів (масиву);
• назва (ідентифікатор) — одна й та сама для всіх елементів масиву;
• розмірність — кількість номерів (індексів), необхідних для визначення розташу­вання елемента у масиві;
• діапазони зміни номерів (індексів).

Cукупність розмірності й діапазонів називають формою масиву.

Звернення до значення елемента масиву у коді програми здійснюють, вказавши після його назви у квадратних дужках індекси у вигляді (арифметичних) виразів, що набувають значень з діапазопу порядкового типу.

Наприклад, а[3] — 3-тій елемент масиву а, с[j] — j-ий елемент масиву с.

Елемент масиву може мати і тип простої (неструктурованої) величини і складений тип (масиву, рядка тощо), тобто може існувати масив масивів, масив рядків тощо. Глибину вкладеності (а значить, і кількість індексів) необмежено, але загальну довжину структури обмежено. У пам'яті ПК всі елементи масиву зберігають послідовно: при переході від молодших до старших адрес першим змінюється індекс, записаний останнім (праворуч).

Порядок роботи з масивом

1. У розділі описів вказати назву, розмір і тип елементів масиву. Це забезпечить (на етапі завантаження програми) виділення потрібного об'єму оперативної пам'яті для зберігання значень елементів.

2. Заповнити комірки пам'яті, виділені для елементів масиву, потрібними значеннями.

3. При потребі вивести масив (на екран, у файл) для наочної перевірки роботи коректності заповнення.

4. Опрацювати масив.

5. Вивести отримані результати.

Під час розв'язування задач переважно використовують одновимірні та двовимірні масиви.

Одновимірний масив інакше ще називають лінійним масивом. Кожному його елементу ставлять у відповідність один індекс. У математиці лінійному масиву відповідає поняття послідовності, а номеру члена послідовності — індекс масиву.

Примітка. Використання масивів розмірності 2 і більше зумовлено лише міркуваннями зручності для програмістів. Наприклад, існує взаємно однозначна відповідність j = kn + l між індексом j — у межах від 0 до (mn – 1) і парою індексів (k, l) при k — у межах від 0 до (m – 1), l — у межах від 0 до (n – 1). А саме: при діленні j на n маємо: k — частка, l — лишок. Аналогічні формули можна вивести і для «зсунутої» (не з нуля) нумерації, і для більших розмірностей.

Форма опису масиву
Var назва масиву : array [розмірність] of тип елементів;

Тут розмірність — перелік діапазонів зміни індексів, розділених комами. Кожен діапазон вказують таким чином:
найменше значення..найбільше значення

Граничні значення індексів вказують явно або як вирази з попередньо визначених сталих.

Мова Pascal не передбачає стандартних засобів введення-виведення усіх елементів масиву однією вказівкою. Тому введення і виведення значень роблять послідовно, окремо для кожного елемента в циклі.

Способи заповнення масиву (подано на прикладі одновимірного масиву a):

• з клавіатури:
  

  for j:=1 to n do       begin
    write('Введіть a[',j,'] ');
    readln(a[j])           end;

• з файлу:
  

  assign(f,'input.txt');         {зв'язування змінної f з назвою файлу input.txt}
  reset(f);                      {відкриття файлу f на зчитування}
  for j:=1 to n do read(f,a[j]); {зчитування значень елементів з 1 до n-го} 
  close(f);                      {завершення роботи з файлом f}

• з використанням генератора випадкових чисел на проміжку [x, y]:
  randomize;
  for j:=1 to n do a[j]:=random(y-x+1)+x;


• за формулою:
  for j:=1 to n do a[j]:=j*(j+1)-1;

3. Вивчення нового матеріалу

Динамічне програмування — розділ математики, який присвячено теорії і методам розв'язання багатокрокових задач оптимального управління на основі використання рекурентних співвідношень.

Поняття рекурентного співвідношення розглянемо на прикладі такої задачі.

Задача 1. Порахувати число послідовностей нулів і одиниць довжини n, в яких не зустрічаються дві одиниці, що йдуть підряд.

Виведення рекурентного співвідношення. Позначимо через K_n шукану кількість. Розглянемо довільну прийнятну послідовність довжини n. Якщо останній її символ дорівнює 0, то перші (n − 1) символ утворюють довільну прийнятну послідовність довжини (n − 1). Кількість таких послідовностей, згідно із запровадженим позначенням, дорівнює всього K_{n − 1}. Якщо останній символ дорівнює 1, то передостанній символ дорівнює 0 (інакше буде дві одиниці підряд), а перші n − 2 символи — довільна прийнятна послідовність довжини n − 2. Число таких послідовностей дорівнює K_{n − 2}. Тому при n > 2 справджується рівність:

K_n = K_{n − 1} + K_{n − 2};
K₁ = 2;
K₂ = 3.

Отримана рівність (зауважте: та сама, що задає послідовність чисел Фібоначчі) виражає залежність члена послідовності K_n для даного значення параметра n через розв'язки для попередніх значень (n − 1) і (n − 2). Таке співвідношення називають рекурентним.

Подамо приклади двовимірного динамічного програмування — задачі про маршрути на прямокутному полі: порахувати число маршрутів або знайти маршрут, які (який) є кращими в деякому сенсі. Для цих завдань характерним є те, що кожний маршрут не може пройти двічі або більше разів однією і тією самою клітиною.

Задача 2. Дано прямокутне поле розміром n × m клітин. Дозволено рухатися полем на одну клітину праворуч або вниз. Порахувати, скількома способами можна потрапити з лівої верхньої клітини у праву нижню.

Виведення рекурентного співвідношення. У клітину поля з координатами (i, j) можна безпосередньо потрапити лише згори або зліва, тобто з клітин з координатами (i − 1, j ) і (i, j − 1). Позначимо через A_ij кількість маршрутів, що ведуть у клітину з координатами (i, j ). Ця величина дорівнює 0 для індексів i, j, що вказують за межі поля. Маємо:

A_ij = A_{(i − 1) j} + A_{i (j − 1)};
A₀₀ = 1.

Задача 3. Дано прямокутний поле розміром n × m клітин. Дозволено рухатися полем на одну клітину праворуч, вниз або по діагоналі праворуч-вниз. У кожній клітині записано деяке натуральне число. Рух розпочинають з верхньої лівої клітки і закінчують у правій нижній. Вагу маршруту обчислюють як суму чисел з усіх відвіданих клітин. Необхідно знайти маршрут з мінімальною вагою.

Виведення рекурентного співвідношення. Позначимо через B_ij найменшу вагу маршруту, що веде у клітину з координатами (i, j ), через с_ij — число, записане у цій клітині. Вважаємо, що B_ij = 0 для індексів i, j, що вказують за межі поля. У клітину з координатами (i, j) можна безпосередньо потрапити лише з клітин з координатами (i − 1, j ), (i − 1, j − 1) і (i, j − 1). Тому маємо:

B_ij = min(B_{(i − 1) j} , B_{(i − 1) (j − 1)} , B_{i (j − 1)}) + c_ij .

Для знаходження оптимального маршруту в окремий масив для кожної клітини потрібно записувати, з якого боку до неї буде зроблено хід. А після визначення значень елементів матриці B маршрут відновити «з кінця».

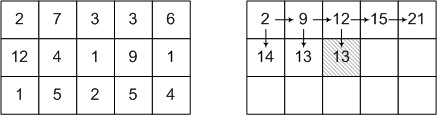
На наступному малюнку подано приклад вихідних даних і одного з кроків алгоритму. Ліворуч зображено таблицю записаних чисел c, праворуч створювану таблицю B. Стрілки вказують, з якого боку необхідно прийти у клітину, щоб отримати мінімальну вагу маршруту у цю клітину.

Розглянемо умову задачі «Банківська справа». Це одна з найпростіших задач, що ілюструє метод динамічного програмування, запропонований Р.Беллманом у 1955 році для задач оптимізації з адитивною цільовою функцієї — функцією зиску для пошуку максимума, функцією втрат для пошуку мінімума. Надалі розглянемо функцію зиску (для пошуку максимума) зі скінченою кількістю варіантів управління. Скінченність забезпечує існування оптимальної рішення.

Адитивність цільової функції означає можливість подання її у такому вигляді:

Тут:

• p_j — певне управлінське рішення. У нашому випадку — скільки монет було дано банкіру j;

• q_j — стан системи після прийняття управлінського рішення p_{j – 1}. У нашому випадку:

  • q₁ = m;
  • q_j = q_{j – 1} – p_{j – 1} при 1 < j;

• значення f_j(q_j, p_j) задано відповідним числом вхідного файлу.

Позначимо через F_n(q₁) максимум цільової функції, записаної вище. Маємо:

У другому рядку внутрішній максимум потрібно шукати за p₁, p₂, …, p_{n – 1}, а зовнішній — за p_n.

У третьому рядку максимум потрібно шукати за q_n і p_n за умови, що стан q_n отримано у результаті прийняття оптимальних управлінських рішень p₁, p₂, …, p_{n – 1}.

Адитивність цільової функції означає можливість подати прийняття рішення про оптимальне керування у вигляді послідовності прийняття рішень p₁, p₂, …, p_{n – 1}, p_n. Інакше кажучи, розв'язання задачі можна розбити на окремі етапи з дотриманням принципу: довільне оптимальне рішення є продовженням оптимального рішення.

Кожний з етапів є окремою частиною поставленої загальної задачі. Їх розв'язують одним і тим самим оптимізаційним алгоритмом. Але розв'язання кожної наступної підзадачі залежить від розв'язків попередньої.

Процес розробки алгоритмів динамічного програмування має такі етапи:

1. Опис структури оптимального розв’язку.
2. Рекурентне визначення оптимального розв’язку підзадач.
3. Обчислення значення цільової функції для оптимального рішення.
4. Отримання оптимального розв’язку.

Динамічне програмування надає математичний апарат для планування багато­крокових керованих процесів чи процесів, які розвиваються у часі. Таким чином, динамічне програмування не є окремим методом розв’язування задач. Це теорія, що поєднує ряд однотипних ідей та прийомів, які застосовують для розв’язування досить різних за змістом задач: оптимальний розподіл капіталовкладень, розподілом продукції між різними регіонами, визначенням найкоротшого шляху завезення товарів споживачам, задачі щодо заміни устаткування, оптимального управління запасами тощо.

Завдання 1. Проаналізувати словесний алгоритм і код розв'язання задачі «Банківська справа». Проаналізувати дію алгоритму (програми) на прикладі вхідних даних з умови.

Для багатьох оптимізаційних задач є простіші й швидші алгоритми. Наприклад, жадібні алгоритми (Greedy algorithm).

Жадібні алгоритми — це загальна назва підходу до вирішення завдань оптимізації. Їх (як і метод динамічного програмування) застосовують у випадках, коли початкову задачу можна розбити на послідовність простіших підзадач, щоб у результаті отримати рішення початкової. У таких алгоритмах роблять вибір, який є найкращим у поточний момент прийняття рішення. Інакше кажучи, здійснюють локально оптимальний вибір, сподіваючись, що він приведе до оптимального рішення глобального завдання. При цьому на кожному кроці вибір повинен бути:

• допустимим, тобто задовольняти обмеженням завдання;
• локально оптимальним;
• остаточним (його не змінюють подальшими кроками алгоритму).

Розглянемо умову завдання ІІІ (міського) етапу олімпіади з інформатики 2005 року «Покриття інтервалами».

Відрізок числової прямої [a₀, b₀] належить об'єднанню скінченної кількості інтервалів [a₁, b₁], [a₂, b₂], …, [a_n, b_n].

Завдання
Створити програму cover.*, яка з даної множини інтервалів вибере найменшу кількість інтервалів, об'єднання яких містить відрізок [a₀; b₀].

Вхідні дані
Файл cover.dat містить у вказаному порядку натуральні числа a₀, b₀, a₁, b₁, …, a_n, b_n, які не перевищують 65432, причому n < 10001.

Вихідні дані
Файл cover.res має містити лише послідовність натуральних чисел a_j(1), b_j(1), a_j(2), b_j(2), …, a_j(k), b_j(k), для якої:

• будь-яка точка відрізка [a₀, b₀] належить щонайменше одному з інтервалів [a_j(1), b_j(1), [a_j(2), b_j(2), …, [a_j(k), b_j(k)];

• нерівності a_j(l) < a_{j(l + 1)} < b_j(l) справджуються при всіх l = 1, 2, …, k – 1;

• a_j(1) < a₀ < b_j(1) i a_j(k) < b₀ < b_j(k).

Вхідні дані ґарантують існування і єдиність розв'язку.

Приклад

Завдання 2. Проаналізувати словесний алгоритм і код розв'язання задачі «Покриття інтер­валами».

Алгоритм розв'язання завдання «Покриття інтервалами»

1. Зчитати вхідні дані.

2. Упорядкувати інтервали покриття за неспаданням правого кінця.

3. Перший інтервал покриття вибирати як інтервал, що містить a₀ і має найбільший номер після проведеного впорядкування.

4. Записати величини меж вибраного інтервалу у вихідний файл.

5. Кожний наступний інтервал покриття вибирати як такий, що містить правий кінець попереднього інтервалу і має найбільший номер. Записати величини меж інтервалу у вихідний файл.

Основними перевагами жадібних алгоритмів є їх простота і невибагливість до ресурсів. Для розглянутого завдання жадібний алгоритм отримує оптимальний розв'язок. У багатьох випадках жадібний алгоритм отримує розв'язок, лише близький до оптимального.

Примітка. Жадібні алгоритми не завжди знаходять глобальний максимум (мінімум). Наприклад, для задачі 2 «Приватні інтереси» із завдання № 7 відбірково-тренувальних зборів команди міста Києва. Точне розв'язання має з дуже короткі алгоритм і код, відмінний від жадібного.

4. Інструктаж з ТВ
5. Вироблення практичних навичок

Завдання 3. Розв'язати задачу «Сходинки», умову якої опубліковано на сайті e-olymp.com/uk/. Здійснити перевірку у режимі online. Результат повідомити учителю.

Завдання 4. Розв'язати задачу «Приватні інтереси», використавши жадібний алгоритм. Пересвідчитися у тому, що для деяких тестів відповідь хибна. Тести запозичити з архіву. Проаналізувати причину розбіжності, уважно перечитавши умову та дію правильного алгоритву для відповідних тестів.

Завдання 5. Дати відповідь на такі питання:

1. Що таке рекурентне співвідношення?
2. Що таке динамічне програмування?
3. До яких задач застосовують динамічне програмування?
4. Що таке жадібний алгоритм?

6. Підбиття підсумків уроку
Виставлення оцінок.

7. Домашнє завдання

1. Вивчити матеріал уроку.
2. При потребі доробити завдання 3, 4.
3. Створити і здати на перевірку online розв'язання задачі про купівлю квитків.

Текст упорядкувала Литвиненко Любов Василівна, вчитель спеціалізованої школи № 148 з поглибленим вивченням української мови та літератури ім. Багряного Дніпровського району міста Києва, під час виконання випускної роботи на курсах підвищення кваліфікації з 12.11.2018 по 16.11.2018.