Комбінаторика: умови задач

Умови задач з комбінаторики

Дороговцев А.Я., Сільвестров Д.С., Скороход А.В., Ядренко М.Й.
Теорія мовірностей. Збірник задач.
За загальною редакцією члена-корреспондента АН УРСР Скорохода А.В.
— Київ, Вища школа, 1976, 384 с. Розділ 1, §2.

З Києва до Чернігова можна дістатися пароплавом, поїздом, автобусом або літаком; з Чернігова до Новгород-Сіверська — пароплавом або автобусом. Скількома способами можна здійснити подорож за маршрутом Київ — Чернігів — Новгород — Сіверський?
На вершину гори веде 7 доріг. Скількома способами турист може піднятись на гору і спуститися з неї? Дати відповідь на те саме запитання, якщо підняття і спуск відбуваються різними шляхами.
У розиграшу першості країни з футбола бере участь 17 команд. Скількома способами можуть бути розподілені золота, срібна і бронзова медалі?
Скільки тризначних чисел можна записати цифрами 0, 1, 2, 3, 4?
Скільки тризначних чисел можна записати цифрами 0, 1, 2, 3, 4, якщо кожну з цих цифр використовувати не більше одного разу?
Скількома способами 7 осіб можуть стати в чергу до каси?
У класі вивчають 10 предметів. У понеділок 6 уроків, причому всі уроки різні. Скількома способами можна скласти розклад на понеділок?
Скільки є п'ятизначних чисел, які діляться на 5?
На одній із бічних сторін трикутника взято n внутрішніх точок, на другій — внутрішніх m точок. Кожну вершину при основі трикутника сполучено прямими з точками, взятими на протилежній бічній стороні. На скільки частин поділитьcя трикутник проведеними прямими?
Скільки партій буде зіграно в шаховому турнірі, якщо кожні два учасники з n зустрінуться один раз?
Скільки діагоналей має опуклий n-кутник?
На площині проведено n прямих ліній, причому жодні дві з них не є паралельними і жодні три не перетинаються в одній точці. Скільки точок перетину утвориться при цьому?
На яке найбільше число частин можуть поділити площину n прямих?
На яке найбільше число частин можуть поділити простір n площин?
На яке найбільше число частин можуть поділити площину n кіл?
На яке найбільше число частин можуть поділити простір n сфер?
Скількома способами можна розставити на шаховій дошці розмірами n × n дві тури різного кольору так, щоб вони не били одна одну?
Автомобільний номер складається з двох літер і чотирьох цифр. Яке число номерів можна скласти, використавши 33 літери кирилиці?
Якщо повернути аркуш паперу на 180°, то цифри 0, 1, 8 не змінюються, 6 і 9 переходять одна в одну, а інші цифри втрачають зміст. Скільки існує семицифрових чисел, величина яких не змінюється при повороті аркуша паперу на 180°?
У розиграшу першості країни з футболу у вищій лізі бере участь 16 команд. Команди, які займають перше, друге і третє місця, нагороджуються від повідно золотою, срібною і бронзовою медалями, а команди, що займуть останні 2 місця, залишають вищу лігу. Скільки різних результатів першості може бути?
1. Скільки різних дільників має число 3⁵ ∙ 5⁴?
2. Нехай р₁, р₂, ..., р_n, — різні прості числа. Скільки дільників має число $p_1^{k_1}\cdot p_2^{k_2}\cdots p_n^{k_n}$?
Пасажир залишив речі в автоматичній камері схову, а коли прийшов забирати речі, то виявив, що він забув номер. Пасажир лише пам'ятає, що в номері були цифри 23 і 37. Щоб відкрити камеру, треба правильно набрати п'ятизначний номер. Яку найбільшу кількість номерів треба перебрати, щоб відкрити камеру?
У прямокутній таблиці з m рядків і n стовпчиків треба записати числа +1 i ‒1 так, щоб добуток чисел у кожному рядку і кожному стовпчику дорівнював 1. Скількома способами це можна зробити?
1. Скількома способами можна з n осіб сформувати команду, яка складається з капітана і (k ‒ 1) члена команди?
2. Довести, що $ kC_n^k =(n-k+1) C_n^{k-1}$.
3. Довести, що $$ C_n^k ={n!\over k! (n-k)!}.$$
Скількома способами можна з 7 осіб вибрати комісію, що складається з 3 осіб?
Скількома способами читач може вибрати 3 книжки з 6?
У скількох точках перетинаються діагоналі опуклого n-кутника, якщо жодні три з них не перетинаються в одній точці?
Розглянемо прямокутну сітку квадратів («шахове місто»), яке складається з m × n прямокутних кварталів, поділених n ‒ 1 «горизонтальними» і m ‒ 1 «вертикальними» вулицями. Скільки є різних найкоротших шляхів на цій сітці сторонами прямокутників, які ведуть з лівого нижнього кута у правий верхній кут — з точки (0, 0) у точку (m, n)?
Використовуючи розв'язання попередньої задачі, довести такі рівності:
1. $C^k_n = C^{k-1}_{n-1} + C^k_{n-1}$.
2. $(C^0_n)^2 + (C^1_n)^2 + \cdots + (C^n_n)^2 = C^n_{2n}$.
3. $C^m_n C^0_k + C^{m-1}_{n-1} C^{1}_{k+1} +\cdots + C^{0}_{n-m} C^{m}_{k+m} = C^m_{n+k+1}$.
4. $C^{r-1}_{n-1} + C^{r-1}_{n-2} +\cdots + C^{r-1}_{r-1} = C^r_{n}$.
Знайти число найкоротших шляхів з точки А до В на шаховій дошці, зображеній на рисунку нижче.
Міжнародна комісія складається з 9 осіб. Матеріали комісії зберігаються в сейфі. Скільки замків повинен мати сейф, скільки ключів до них треба виготовити і як їх розподілити серед членів комісії, щоб доступ до сейфа був можливий тоді і лише тоді, коли збереться не менше 6 членів комісії? Розглянути задачу для випадку, коли комісія складається з n осіб, а сейф можна відкрити лише при наявності не менше m членів комісії.
В опуклому n-кутнику проведено всі діагоналі. Відомо, що жодні три з них не перетинаються в одній точці. На скільки частин поділиться при цьому многокутник?
Довести, що $$(a + b)^n = \sum\limits_{k=0}^n C^k_n a^{n-k} b^k.$$
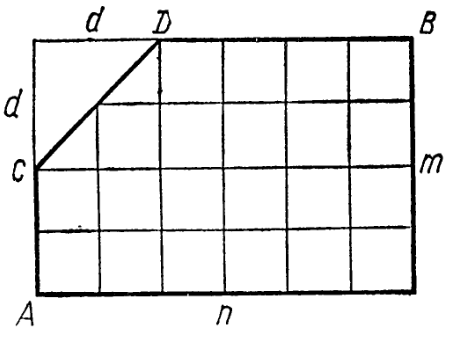
1. Довести, що $C^{k+1}_n>C^k_n$ при k < (n ‒ 1)/2 і $C^{k+1}_n < C^k_n$ при k < (n ‒ 1)/2.
2. Вказати найбільше число серед чисел $C^k_n$, де k = 0, 1, 2, ..., n.
Знайти n, якщо відомо, що в розкладі (1 + x)ⁿ коефіцієнти при x⁵ та x¹² однакові.
Скільки раціональних членів містить розклад $(\sqrt{2} + \sqrt[4]{3})^{100}$.
Довести, що числа $ C^1_p$, $C^2_p$, ..., $C^{p-1}_p$ кратні p, якщо p — просте число.
Довести, що різниця $a^p-a$ при будь-якому цілому a кратне p, якщо p — просте число (мала теорема Ферма).
Довести, що різниця $[(2 + \sqrt{5})^p]-2^{p+1}$ кратне p, якщо p — просте число і p > 2. Тут [x] позначає цілу частину x.
Скільки підмножин має множина, що містить n елементів? Вважати, що порожня множина є підмножиною кожної множини.
У кімнаті n лампочок. Скільки всього є різних способів освітлення кімнати, при яких горить рівно k лампочок? Скільки всього може бути різних способів освітлення кімнати?
Є мережа доріг (див. рис. нижче). З точки А виходить 2ⁿ туристів, причому половина йде в напрямі l, а половина — в напрямі m. Дійшовши до першого перехрестя, кожна група поділяється на дві групи: половина йде в напрямі l, половина — в напрямі m. Такий самий поділ відбувається на кожному перехресті. Де будуть перебувати всі ці туристи після того, як пройдуть n відрізків, і скільки туристів виявиться на кожному перехресті?
На площині дано n точок, причому m точок лежить на одній прямій і крім них жодні три точки не лежать на одній прямій. Скільки існує трикутників, вершинами яких є дані точки?
Скількома способами можна розмістити на полиці 4 книги?
Скількома способами можна впорядкувати множину {1, 2, ..., 2n} так, щоб кожне парне число мало парний номер?
Скільки можна зробити перестановок з n елементів, у яких дані 2 елементи не стоять поруч?
Скількома способами можна розмістити на шаховій дошці 8 однакових тур так, щоб вони не могли бити одна одну?
Скількома способами можна розсадити 4 учнів на 25 місцях?
Студентові потрібно за 8 днів скласти 4 іспити. Скількома способами це можна зробити?
Скількома способами можна впорядкувати множину 1, 2, ..., n так, щоб числа 1, 2, 3 стояли поруч і у порядку зростання?
Скільки існує натуральних чисел, менших за 10ⁿ, цифри яких різні й розміщені у порядку зростання?
Скільки існує перестановок з n елементів, серед яких між двома даними елементами стоїть r елементів?
На зборах повинно виступити 4 особи: А, В, С, D. Скількома способами їх можна записати у список ораторів, якщо В не може виступити раніше, ніж А?
Скількома способами можна розмістити n гостей за круглим столом?
Скількома способами можна впорядкувати множину {1, 2, ..., n} так, щоб кожне число, кратне 2, і кожне число, кратнe 3, мало номер, кратний 2 і 3?
Скільки різних слів можна утворити переставлянням літер у слові «математика»?
Нехай маємо n літер: k₁ — літер a₁, k₂ — літер a₂, ..., k_m — літер a_m, де k₁ + k₂ + ... + k_m = n. Скільки різних слів можна утворити з цих літер?
Скільки слів з п'яти літер можна утворити з літер a, b, c, якщо відомо, що літера а зустрічається у слові не більше двох раз, b — не більше одного разу, с — не більше трьох раз?
Скільки різних слів можна утворити переставлянням букв у слові «комбінаторика»?
Скількома способами можна поділити k + l + m предметів на три групи так, щоб в одній групі було k предметів, у другій — l, у третій — m предметів?
Скількома способами можна поділити 3n різних предметів між трьома особами так, щоб кожна особа одержала n предметів?
Довести поліномінальну теорему:$$(a_1 + a_2 + \cdots + a_k)^n = \sum\limits_{0\leq n_1,~0\leq n_2,~...,~0\leq n_k\\n_1 + n_2 + \cdots + n_k = n} {n! \over n_1! n_2! \cdots n_k!} a_1^{n_1} a_2^{n_2} \cdots a_k^{n_k}.$$
n однакових куль розміщують у N урнах. Довести, що:
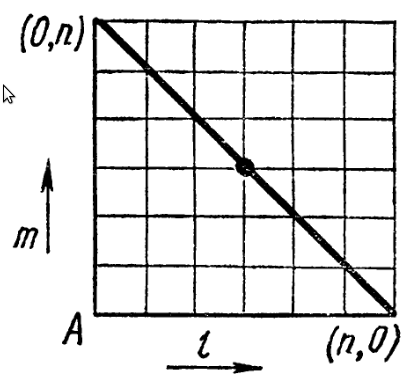
1. Число різних способів розміщення дорівнює $C^n_{N+n-1}=C^{N-1}_{N+n-1}$.
2. Число розміщень, при яких в кожній урні є принаймні одна куля, дорівнює $C^{N-1}_{n-1}$.
1. Скільки розв'язків у цілих невід'ємних числах має рівняння x₁ + x₂ + ... + x_N = n?
2. Скільки розв'язків у цілих додатних числах має це рівняння?
Нехай є аналітична функція N змінних f (x₁, x₂, ..., x_N). Скільки різних частинних похідних порядку n має ця функція?
У першоджерелі немає задачі під цим номером.
Скількома способами можна розподілити n однакових подарунків серед N дітей? Скільки серед них таких способів, коли кожна дитина одержує принаймні один подарунок?
Комбінації з m предметів по n з повтореннями — це групи по n предметів, узятих з даних m предметів, причому, кожен предмет може повторюватись будь-яке число разів. Порядок предметів у групі не є істотним. Написати всі комбінації з трьох елементів по 2 з повтореннями. Довести, що число комбінацій з повтореннями з m елементів по n дорівнює $C_{m+n-1}^{m-1}$.
Скількома способами можна вибрати 6 однакових або різних тістечок в кондитерській, де є 11 різних сортів тістечок?
Скільки костей доміно можна утворити, використовуючи числа 0, 1, ..., r?
Скільки розв'язків у цілих невід'ємних числах має нерівність: x₁ + x₂ + ... + x_m ≤ n, де n — ціле невід'ємне число?
Скільки розв'язків у цілих невід'ємних числах має система нерівностей:

x₁ ≤ r + 1;

x₁ + x₂ ≤ r + 2;

.....................................

x₁ + x₂ + ... + x_n ≤ r + n,
де r — ціле невід'ємне число.
Нехай є множина A = {a₁, a₂, ..., a_n} з n елементів, яку називатимемо генеральною сукупністю, і нехай послідовно з множини А вибирають r елементів $a_{i_1},~ a_{i_2},~...,~a_{i_r}$. Послідовність $a_{i_1},~ a_{i_2},~...,~a_{i_r}$ називатимемо вибіркою довжини r з генеральної сукупності А. Розглянемо два способи вибору: вибір з поверненням (кожного разу взятий елемент повертають до А) та вибір без повернення (кожного разу взятий елемент не повертають до А). Довести, що число різних вибірок довжини r з генеральної сукупності (яка містить n елементів) дорівнює:
- n^r, якщо здійснюють вибір з поверненням;
- $A^r_n$, якщо здійснюють вибір без повернення.
Нехай множина X містить k елементів, а множина Y — n елементів. Скільки є різних функцій з областю визначення X і областю значень Y?
Нехай |А| — число елементів множини А. Довести, що:
1. | A₁ ∪ A₂ | = | A₁ | + | A₂ | ‒ | A₁ ∩ A₂ |;
2. | A₁ ∪ A₂ ∪ A₃ | = | A₁ | + | A₂ | + | A₃ |
  ‒ | A₁ ∩ A₂ | ‒ | A₁ ∩ A₃ | ‒ ... ‒ | A₂ ∩ A₃ | + | A₁ ∩ A₂ ∩ A₃|
3. | A₁ ∪ A₂ ∪ ... ∪ A_n | = | A₁ | + | A₂ | + ... + | A_n |
  ‒ | A₁ ∩ A₂ | ‒ | A₁ ∩ A₃ | ‒ ... ‒ | A₁ ∩ A_n | ‒ | A₂ ∩ A₃ | ‒ | A₂ ∩ A₄ | ‒ ... ‒ | A_{n ‒ 1} ∩ A_n |
  + | A₁ ∩ A₂ ∩ A₃| + | A₁ ∩ A₂ ∩ A₄| + ... + | A_{n ‒ 2} ∩ A_{n ‒ 1} ∩ A_n |
  ‒ | A₁ ∩ A₂ ∩ A₃ ∩ A₄| ‒ | A₁ ∩ A₂ ∩ A₃ ∩ A₅| ‒ ... ‒ | A_{n ‒ 3} ∩ A_{n ‒ 2} ∩ A_{n ‒ 1} ∩ A_n | + ...
  + (‒1)^{n ‒ 1} | A₁ ∩ A₂ ∩ ... ∩ A_{n ‒ 1} ∩ A_n |, де:
  - спочату здіснено додавання за всіма множинами;
  - потім — віднімання за всіма неупорядкованими парами різних множин, кількість яких дорівнює $C_n^2$;
  - потім — додавання за всіма неупорядкованими трійками різних множин (при n ≥ 3), кількість яких дорівнює $C_n^3$;
  - потім — віднімання за всіма неупорядкованими четвірками різних множин (при n ≥ 4), кількість яких дорівнює $C_n^4$ ...
  В останньому рядку записано кількість елементів перетину всіх множин з точністю до знаку. Кількість усіх членів правої частини рівності дорівнює кількості непорожніх підмножин n-елементної множини, тобто 2^{n ‒ 1}.
Учні побували на екскурсії. Всі вони були або зі значками, або в галстуках. Хлопців було 16, учнів зі значками 24. Дівчат з галстуками було стільки, скільки хлопців зі значками. Скільки учнів було на екскурсії?
У класі 35 учнів. З них 20 відвідують математичний гурток, 11 — фізичний, а 10 учнів не відвідуютьжодного гуртка. Скільки учнів відвідують математичний та фізичний гуртки? Скільки учнів відвідують лише математичний гурток?
Із 100 студентів англійську мову знають 28 студентів, німецьку — 30, французьку — 42, англійську і німецьку — 8, англійську і французьку — 10, німецьку і французьку — 5, всі з мови знають 3 студенти. Скільки студентів не знають жодної з трьох мов?
У жорстокому бою не менше 70% бійців втратили одне око, не менше 75% — одне вухо, не менше 80% — одну руку і не менше 85% — одну ногу. Яка мінімальна кількість бійців, які втратили одночасно око, вухо, руку й ногу? (Льюис Кэррол. История с узелками. М., «Мир», 1973.)
Розглядають усі перестановки n чисел 1, 2, ..., n. Знайти число тих перестановок, у яких принаймні одне число стоїть на своєму місці.
Нехай а₁, а₂, ..., а_n — взаємно прості натуральні числа, а N — деяке натуральне число. Знайти число додатних натуральних чисел, які не перевищують N і не діляться на жодне з чисел а₁, а₂, ..., а_n.
Нехай n — натуральне число, розклад на прості множники якого має вигляд $n = p_1^{n_1} p_2^{n_2}\cdots p_k^{n_k}$ (p₁, p₂, ..., p_k — прості числа), а $\varphi (n)$ — число додатних натуральних чисел, які не перевищують n і взаємно прості з n (функцію $\varphi (n)$ називають функцією Ейлера). Довести, що $$\varphi (n) = p \left( 1-{1\over p_1}\right)\left( 1-{1\over p_2}\right) \cdots \left( 1-{1\over p_k}\right)$$.
Скільки членів у розкладі визначника n-го порядку містять один або більше діагональних елементів?
Нехай $N_{[m]} (A_1 \cup A_2 \cup \cdots \cup A_n)$ — число елементів, які входять рівно в m множин з A₁, A₂, ..., A_n. Довести, що $$ N_{[m]} (A_1 \cup A_2 \cup \cdots \cup A_n) =\\ C^m_m \sum\limits_{1\leq i_1\leq i_2 \leq \cdots \leq i_m \leq n} |A_{i_1} \cap A_{i_2} \cap \cdots \cap A_{i_m}|\\ - C^m_{m+1}\sum\limits_{1\leq i_1\leq i_2 \leq \cdots \leq i_{m+1} \leq n} |A_{i_1} \cap A_{i_2} \cap \cdots \cap A_{i_{m+1}}| + \cdots\\ + (-1)^{n-m} C^m_n \sum\limits_{1\leq i_1\leq i_2 \leq \cdots \leq i_n \leq n} |A_{i_1} \cap A_{i_2} \cap \cdots \cap A_{i_n}|.$$
Знайти число всіх перестановок чисел 1, 2, ..., п, в яких m чисел стоять на своїх місцях.
Нехай A — множина п елементів, A₁, A₂, ..., A_k — підмножини А такі, що жодна з підмножин не є частиною іншої. Довести, що $k\leq C^{[n/2]}_n$ (теорема Шпернера).
Нехай A — множина з п елементів, A₁, A₂, ..., A_k — підмножини А такі, що жодна з підмножин не є частиною іншої, а i₁, i₂, ..., i_k — кількість елементів множин A₁, A₂, ..., A_k. Довести, що $$\sum\limits_{r=1}^k {1\over C^{i_r}_n} \leq 1.$$
Нехай x₁, x₂, ..., x_n, 1 ≤ |x_k|. Довести, що тоді у будь-якому інтервалі довжини 2 є не більше $C_n^{[n/2]}$ сум вигляду $\sum\limits_{r=1}^n \varepsilon_r x_r$, де $\varepsilon_k = \pm 1$. .
Нехай A₁, A₂, ..., A_s — підмножини множини п елементів такі, що немає множин A_i та A_j, для яких A_i ⊃ A_j і A_i \ A_j містить більше, ніж (r ‒ 1) елемент. Довести, що тоді s не перевищує суму r найбільших за величиною біномних коефіцієнтів $C^k_n$.
Нехай r — довільне ціле число,x₁, x₂, ..., x_n — дійсні числа, x_k > 1 (k = 1, 2, ..., n.) Довести, що який би не був інтервал довжини 2r, число сум вигляду $\sum\limits_{r=1}^n \varepsilon_r x_r$, де $\varepsilon_k = \pm 1$, що лежать в цьому інтервалі, не перевищує суми найбільших біномних коефіцієнтів $C^k_n$.